Association Méridienne
Atelier
Astrolabe planisphérique
L'araignée
- Pour en savoir plus
- Astrolabe planisphérique
- Historique de l'astrolabe
- Différentes parties
- Calculs pour la construction d'un astrolabe:
- 1- le tympan
- 2- l'araignée
- 3- l'ostenseur
- 4- Le limbe
- 5- Le verso de la mère
- 6- l'alidade
- Construction d'un astrolabe
- Utilisation d'un astrolabe
- À admirer: un astrolabe construit à partir des travaux de Méridienne
- Bibliographie et webographie
L'araignée
L'écliptique
-
Diamètre de l'écliptique
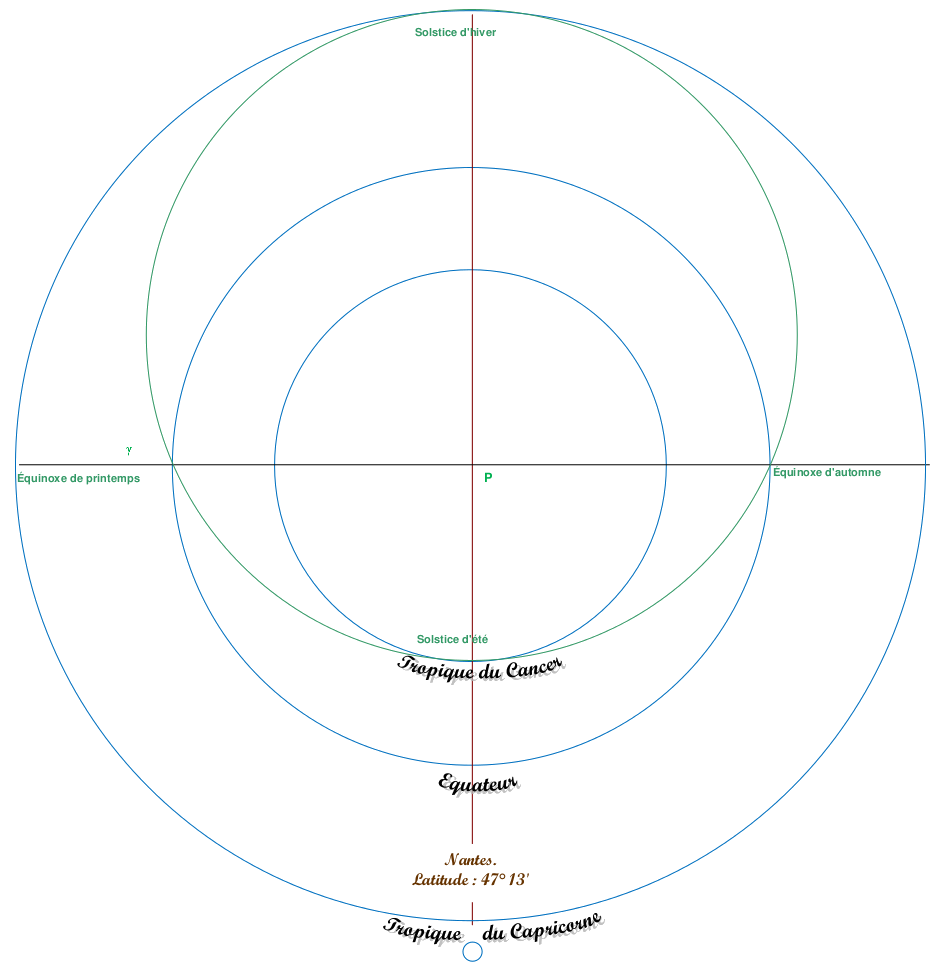
Le cercle de l'écliptique est la trajectoire du Soleil sur la voûte céleste durant l'année.
Il est situé entre les deux tropiques. Il est tangent au tropique du cancer au solstice d'été et tangent au tropique du capricorne au solstice d'hiver.
Décliptique = Rtropique du capricorne + Rtropique du cancer
Décliptique = 4,09 + 9,5
Décliptique = 13, 59 cm
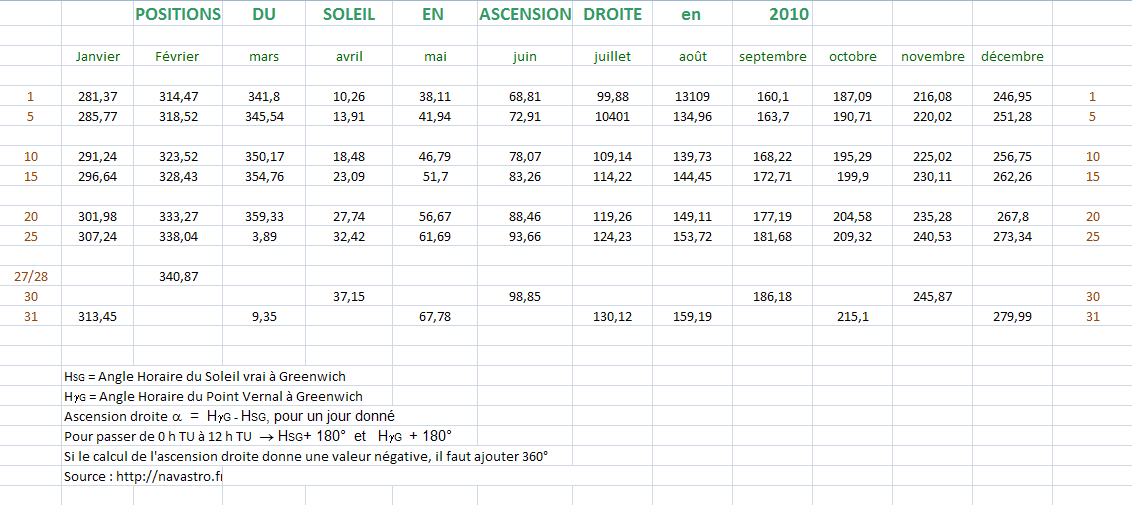
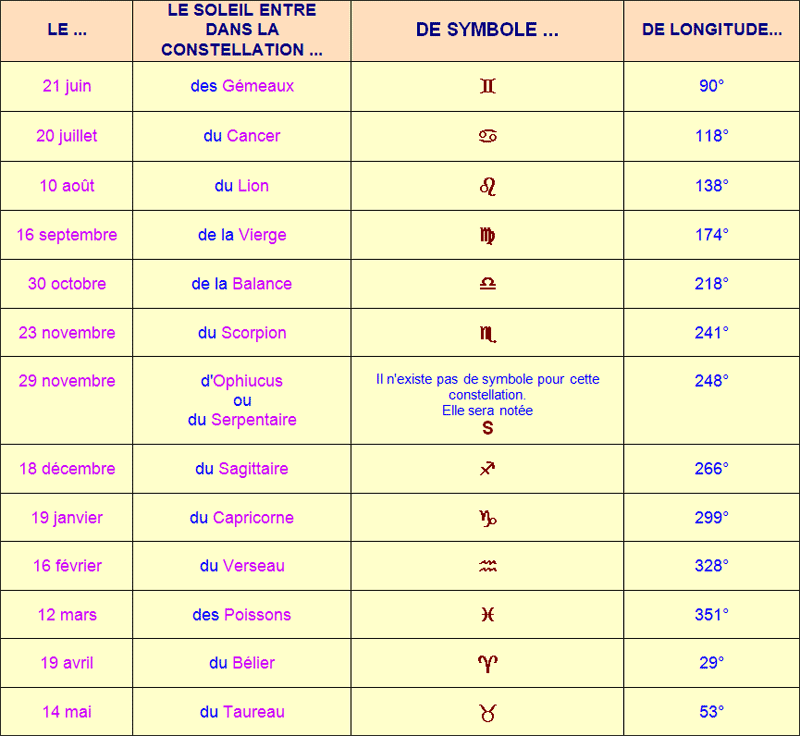
Tracés des dates sur l'écliptique
Les constellations zodiacales
En raison de la précession, les limites entre les constellations zodiacales sur l'écliptique se décalent de
0,013 969° par an, soit
1° tous les 71,6 ans
,
30° tous les 2 147,5 années
et
360°
tous les 25 770,5 ans
. Cependant, ce calcul suppose que le taux de précession annuel est constant sur 26 millénaires, ce qui n'est pas le cas.
En réalité ce taux est lentement croissant, du moins pour les quelques millénaires à venir. C'est pourquoi, la valeur arrondie de
360° en environ 26 000 ans
est souvent retenue.
La précession des équinoxes est le lent mouvement rétrograde du point γ sur l'écliptique, c'est-à-dire dans le sens des
aiguilles d'une montre qui serait posée sur le plan équatorial, cadran vers le nord (alors que le Soleil se déplace dans le sens direct).
Le point γ "visite" ainsi successivement toutes les constellations zodiacales en 26 000 ans. Il se trouvait dans la constellation du
Taureau au temps du vieil empire babylonien (2500 av. J.-C.), et dans celle du Bélier à l'époque d'Hipparque (IIe siècle av. J.-C.).
Il est de nos jours dans la constellation des Poissons.
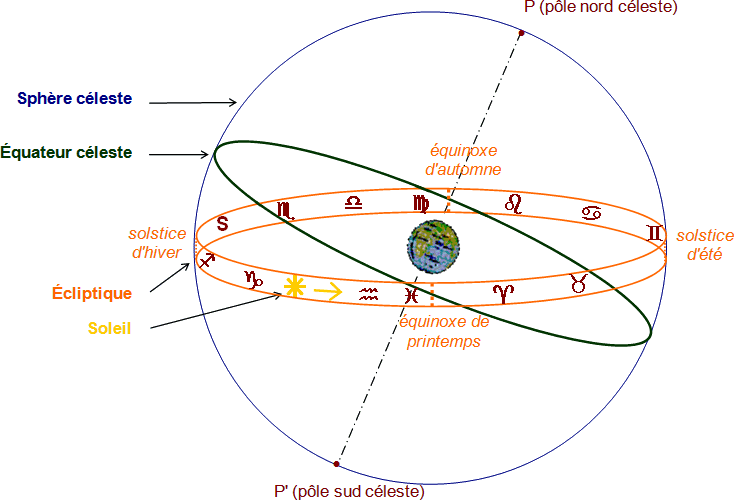
La sphère céleste et la position des constellations zodiacales.
La position des étoiles
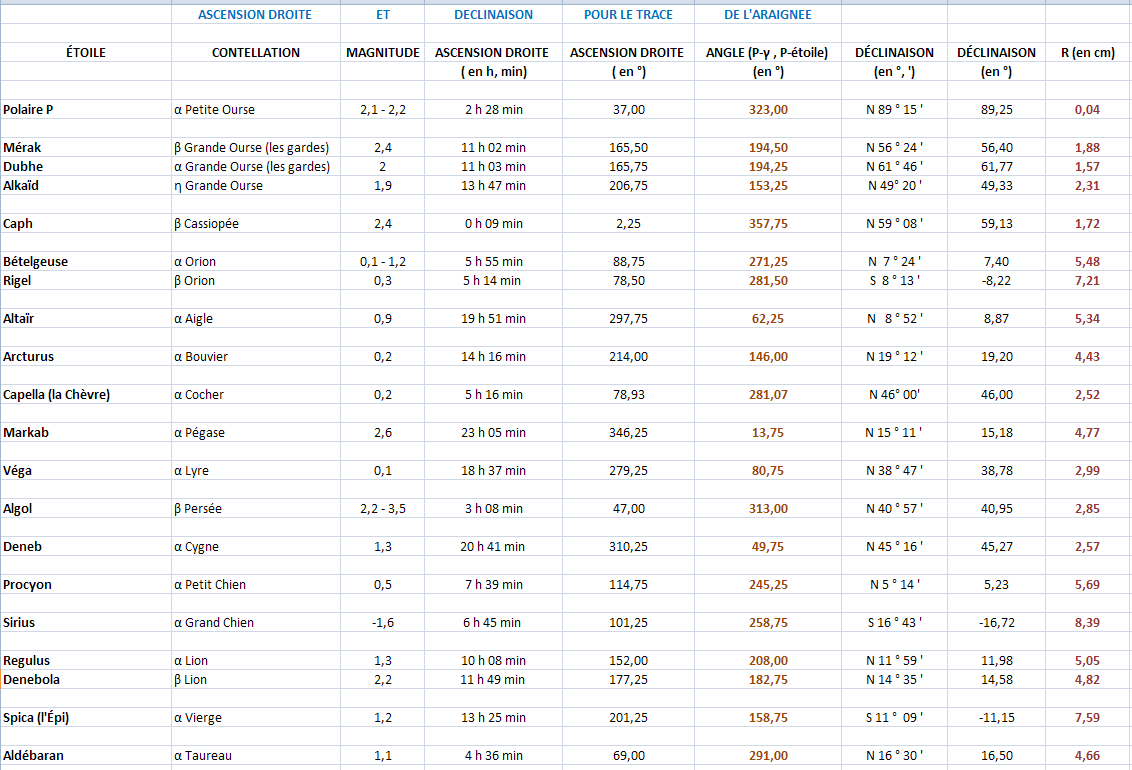
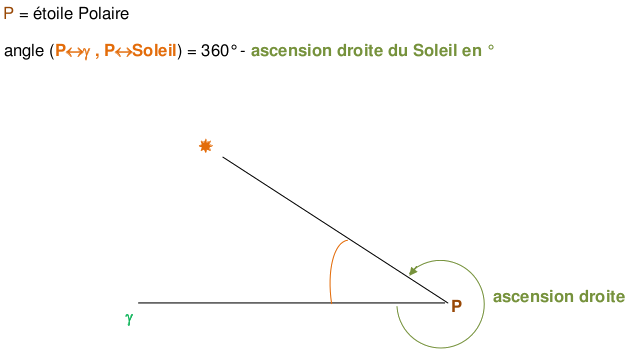
- P = étoile Polaire
angle (P «--»γ , P «--»étoile) = 360° - ascension de l'étoile en ° - \(\text{d(P, étoile)} = \text{R}_\text{étoile} = \text{R}_\text{équateur} \times \tan \dfrac{90° - \text{déclinaison}}{2} = \text{R}_\text{équateur} \times \tan \dfrac{90° - \delta}{2}\)
\(\text{R}_\text{étoile} = 6,24 \times ( \tan{45° - \dfrac{\delta}{2}}) \)
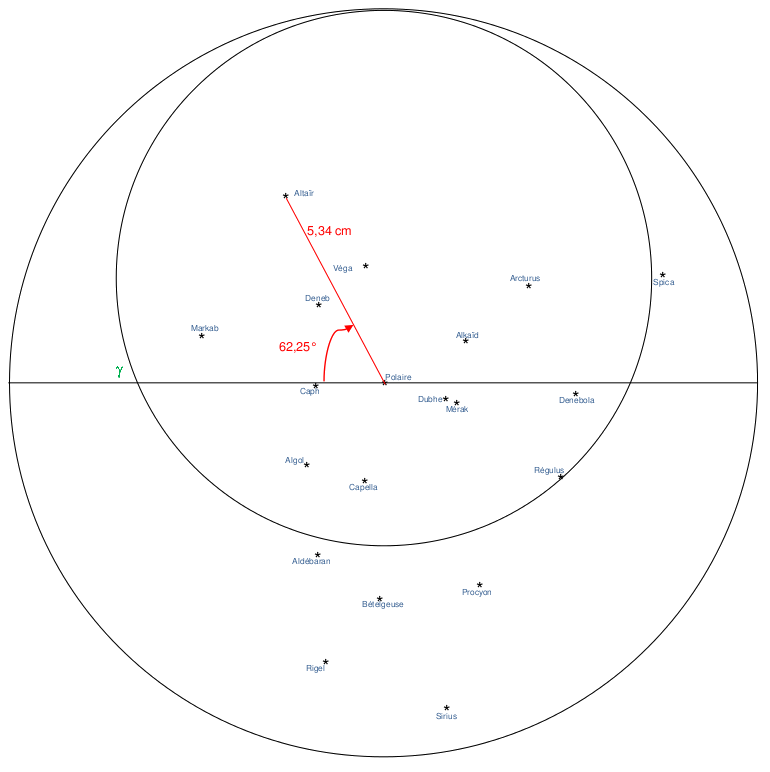
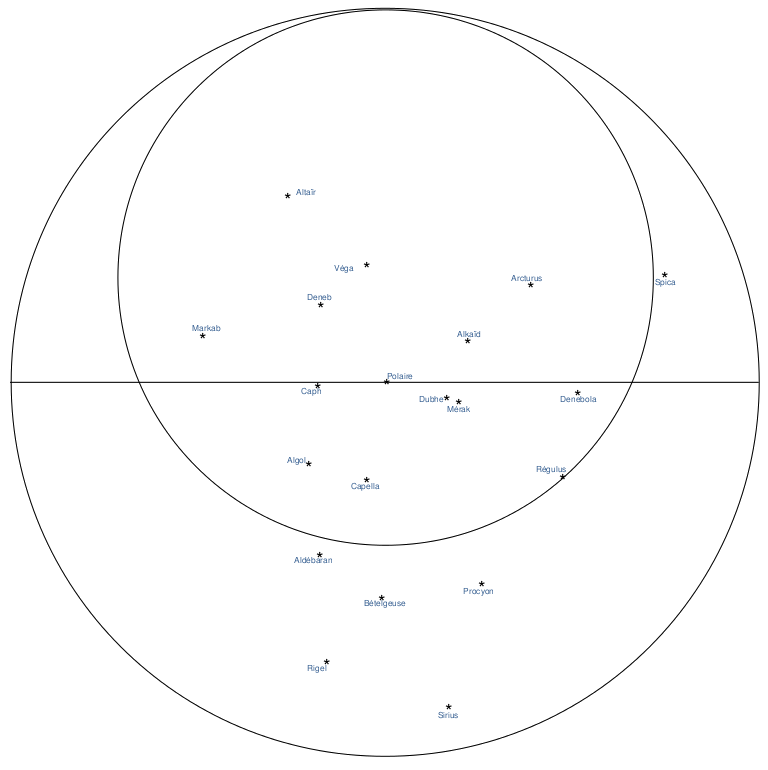
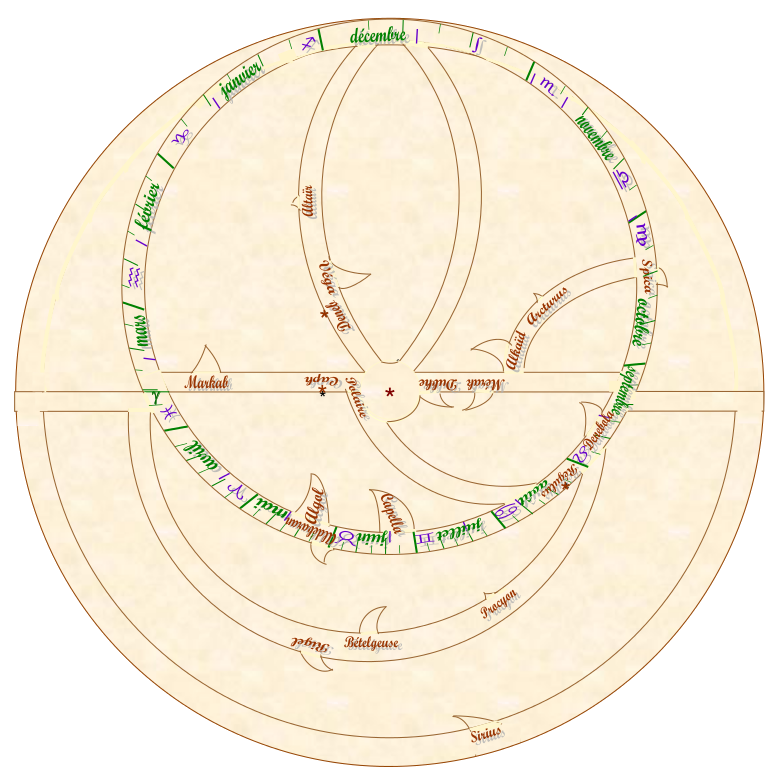
Araignée finie pour impression
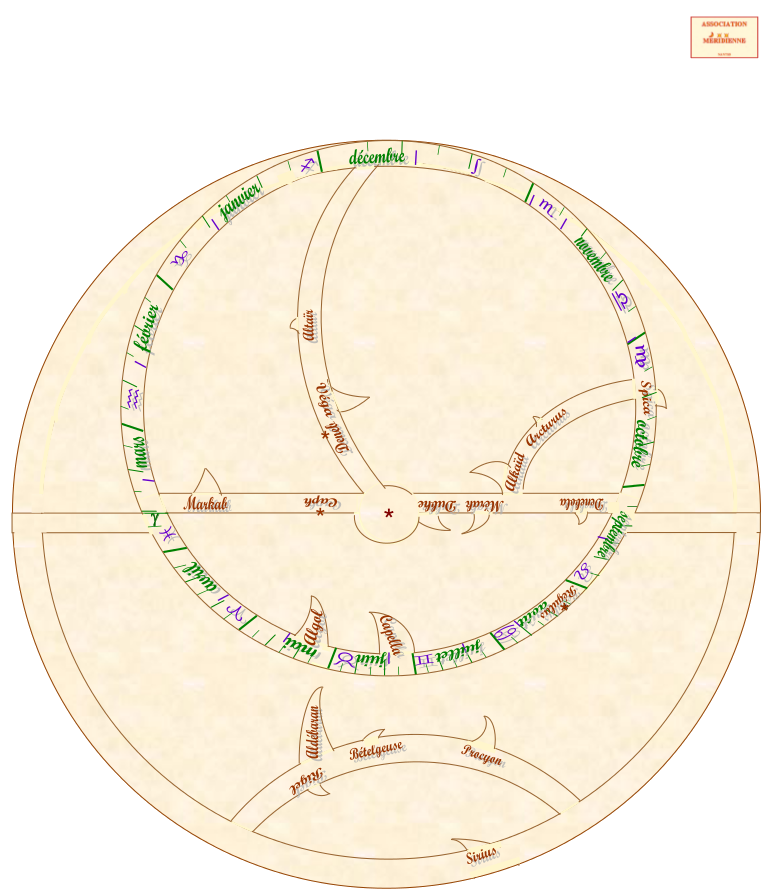
ou
