
Dernière mise à jour: 1er avril 2024
Bienvenue sur le site de l'association Méridienne
14ème rencontre des Coques en Bois à Pornic

Invitée par l'association Coques en bois, l'association Méridienne expose et commente ses re-créations d'instruments d'astronomie et de navigation.
Pornic, le vieux port, les 22 et 23 juin 2024.
La longitude en mer par les distances lunaires
Aperçu historique et présentation des principales méthodes mathématiques employées du XVIIIe au XXe siècle

La longitude en mer par les distances lunaires de Paul Bedel est le 13ème volume de la collection du Bureau des longitudes.
Vous pouvez le consulter en ligne à cette adresse:
https://site.bdlg.fr/wp-content/uploads/2024/03/Coll-BDL-vol-13.pdf
Parcours astronomique

L'association Méridienne propose un parcours consacré à l’astronomie à Nantes sur Nantes patrimonia.
Rues aux noms d'astronomes, objets patrimoniaux et lieux de sciences jalonneront votre trajet virtuel ou réel.
Cérémonie de remerciements pour les journées du Patrimoine et du Matrimoine

Lors de la cérémonie de remerciements pour les journées du Patrimoine et du Matrimoine, l'adjoint Olivier Chateau a rendu un hommage particulier à Méridienne pour sa participation à ces journées depuis plus de 10 ans.
Du nouveau à propos du méthéoroscope
Le 9 mars 2023 a été publié en ligne un article intitulé Ptolemy’s treatise on the meteoroscope recovered portant sur l'étude par l'imagerie multi-spectrale d'un manuscrit latin du VIIIe siècle.
Voir Historique du méthéoroscope géographique.
Navigation astronomique

Navigation astronomique, une étude de Méridienne, avec des droites de hauteur réalisées à bord du porte-hélicoptère Jeanne d'Arc par le Contre-amiral Bernard Jacquet.
Les sextants français, une étude de Yvon Petitbon, adhérent de Méridienne.
Le bureau des longitudes en société

Le bureau des longitudes en société est le 12ème volume de la collection du Bureau des longitudes.
Vous pouvez le consulter en ligne à cette adresse:
https://site.bdlg.fr/wp-content/uploads/2022/11/Volume-12.pdf.
Golden Globe Race 2022
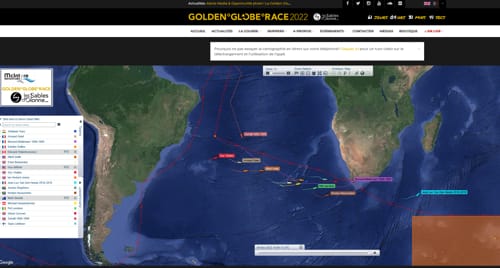
Suivez en direct la Golden Globbe Race 2022 sur leur site:
https://goldengloberace.com/fr/
L'énigmatique traité de navigation sur Patrimonia

Le service patrimoine de la Bibliothèque municipale de Nantes possède dans ses fonds, sous la cote Ms482, un magnifique manuscrit d’un Traité de la navigation de 1705.
Nantes Patrimonia présente ce traité, en lien avec des reconstitutions d'instruments de Méridienne.
https://patrimonia.nantes.fr/home/actualites/un-enigmatique-traite-de-la-navi.html
De nouveaux instruments


La commission atelier instrumental et documentaire présente deux nouveaux instruments de navigation astronomique: l'astrolabe portugais et le spiegelboog .
Exposition terre! terre!
Les conquêtes européennes au 16e siècle
Du 9 avril au 6 novembre 2022, au château de Kerjean, 29440 Saint-Vougay

Méridienne a prêté les re-créations d'une boussole et d'une sonde pour cette exposition.
L'horloge marine de Méridienne

La commission atelier instrumental et documentaire présente l'horloge marine de Méridienne, d'après l'horloge H1 de J. Harrison.
Le loch à hélice

Une étude de Yvon Petitbon, Le loch à hélice, a été ajoutée à la section Ressources.
Villeneuve en Retz, ville étoilée 3 étoiles

Samedi 18 décembre, au Musée du Pays de Retz de Bourgneuf, la commune de Villeneuve en Retz a reçu le label Villes et Villages Étoilés (trois étoiles).
Ce label, créé par l'ANPCEN (Association Nationale pour la protection du Ciel Nocturne), récompense les communes engagées dans une démarche d'amélioration de
la qualité de l'environnement nocturne. Villeneuve en Retz et Clisson sont actuellement les seules communes labellisées dans le département de Loire-Atlantique.
Le Musée du Pays de Retz et l'association des Randonneurs des Étoiles ont évoqué avec Méridienne, invitée à la remise du label, la poursuite d'activités communes.
Prix de la Maison de la Mer - Daniel Gilard 2021
Vendredi 15 octobre, Jean-Pierre Arcile, Peintre Officiel de la Marine, a reçu le Prix de la Maison de la Mer - Daniel Gilard 2021.

Jean-Pierre Arcile avait réalisé la maquette de la carte de l'association Méridienne. Nous lui adressons nos chaleureuses félicitations.
Femmes astronomes, elles ne courent pas les rues.

Vous trouverez, dans le numéro de septembre 2021 de L'ASTRONOMIE un article de Colette Le Lay, notre secrétaire, sur les femmes astronomes.
Voir Place Edmée Chandon, étape 3 du parcours n°5.
Panneau et flamme

Notre vice-président Olivier Sauzereau présente nos nouveaux outils de communication: flamme drapeau, panneau de présentation, flyers, marque-pages.
L'Annuaire du Bureau des longitudes
Le volume 8 de la collection du Bureau des longitudes, l'Annuaire du Bureau des longitudes, de Colette Le Lay, secrétaire de Méridienne est désormais disponible en pdf sur le site du Bureau des longitudes.

Dès les origines, la composition d’un Annuaire « propre à régler ceux de toute la République » fait partie du cahier des charges du Bureau des longitudes. Au calendrier sont rapidement adjointes de multiples tables puis des Notices scientifiques, conférant à l’Annuaire un statut de revue de vulgarisation au lectorat fidèle. Au fil des soubresauts de l’histoire, l’Annuaire, largement diffusé en France et à l’étranger, évolue tout en conservant son identité.
Olivier Sauzereau dans le hors-série de la revue l’éléphant

Olivier Sauzereau, notre vice-président, a participé au hors-série Mythologie de la revue l’éléphant que vous pouvez trouver chez votre marchand de journaux, votre libraire ou en commandant grâce au lien ci-dessus. Bonne lecture !
Le Bureau des longitudes son histoire et ses travaux
des origines (1795) à ce jour

Créé par la Convention en 1795, le Bureau des longitudes poursuit son chemin de petite académie pluridisciplinaire en ce XXIe siècle. L’ouvrage (photo ci-dessus), qui rejoint la bibliothèque de Méridienne, rassemble en un seul volume les Notices de l’Annuaire du Bureau des longitudes publiées entre 1928 et 1933 par Guillaume Bigourdan pour retracer l’histoire de cette institution dont il était membre.
L'édition a été préparée par Nicole Capitaine et Colette Le Lay, secrétaire de Méridienne, en collaboration avec Guy Boistel.
Tables de navigation 1840-1980, de Paul Bedel

Après avoir suivi la formation de Capitaine de 1e classe de la Navigation maritime à l’Ecole nationale de la Marine Marchande du Havre, Paul Bedel a navigué en tant qu’officier à la Compagnie générale maritime. Il a ensuite opté pour l’enseignement maritime ; d’abord comme professeur à l’ENMM du Havre puis directeur d’ENMM et enfin en tant qu’Inspecteur général de l’Enseignement maritime.
Il vient de publier une étude sur les Tables de navigation (1840-1980), Collection du Bureau des longitudes, vol.5 (août 2020). Cet ouvrage est consultable en ligne sur https://site.bdlg.fr/wp-content/uploads/2020/07/BDL4_Bedel.pdf
Dans ses remerciements, l'auteur cite notre ami Yvon Petitbon, dont il fut l’élève au Havre.
Paul Bedel a honoré Méridienne par la remise de l’un des rares exemplaires imprimés de son ouvrage. Nous le joignons avec plaisir à notre fonds documentaire et nous l’en remercions.
Retrouvez les parcours scientifiques Méridienne sur Nantes patrimonia
- Un mix des parcours 1 et 2 : Parcours scientifique
- Le parcours 3 : Médéric-Clément Lechalas
Le dictionnaire professionnel maritime

Les presses universitaires de Rouen et du Havre viennent de publier le dictionnaire professionnel maritime, de Laurent Galy.
On y trouvera la photo d'une des re-créations de Méridienne.
Histoire de navires dans la Chine ancienne

Les Éditions Ancre de marine (Saint-Malo) viennent de publier le livre du professeur Xi Long Fei : Histoire des navires dans la Chine ancienne.
Ce livre a été traduit du chinois par Christian A. Fardel, adhérent de Méridienne.
La règle à calcul, de Marc Thomas
La règle à calcul - La longue histoire d’un instrument oublié, de Marc Thomas, membre de l'association Méridienne, vient de paraître aux Presses Universitaires de Limoges.
Cadran Info
Cadran Info N° 33 (mai 2016) de la Commission des Cadrans Solaires (CCS) de la Société d'Astronomie de France (SAF) présente le dossier réalisé par l'association Méridienne sur le cadran solaire dit de Kratzer.

Le dossier réalisé par l'association Méridienne
Dictionnaire de Nantes
Deux adhérents de Méridienne ont contribué au Dictionnaire de Nantes dans lequel ils ont rédigé les articles École d'hydrographie, Museum, Observatoire et Scientifique (patrimoine).

Dictionnaire de Nantes, s/d Alain Croix, Presses Universitaires de Rennes, 2013
L'association Méridienne a participé à :
Festival "De la terre aux étoiles", à Nantes
Du 13 au 28 janvier 2024

1er festival d'astronomie à Nantes
La fête de la science 2023, à Nantes
6, 7 et 8 octobre 2023

Au Museum d'histoire naturelle:
Naviguer sans GPS, c’est du sport !
Les journées du patrimoine 2023 à Nantes
les 16 et 17 septembre 2023

- Exposition et démonstration d'instruments de navigation et d’astronomie des origines à nos jours recréés.
- Exposition présentant les parcours de quelques femmes pirates et corsaires nantaises et de femmes astronomes.
- Visites commentées de la tour de l’ancien observatoire de la marine.
Festival d'astronomie de la Chapelle aux Lys 2023
19 et 20 août 2023

Exposition de re-créations d'instruments de navigation et d'astronomie..
La 13ème rencontre de 'Coques en bois', à Pornic (44).
17 et 18 juin 2023

Exposition de re-créations d'instruments de navigation et d'astronomie.
La fête de la science 2022, à Nantes
7, 8 et 9 octobre 2022

Au Museum d'histoire naturelle:
Trouver sa longitude sur l'océan.
Intervention à Saint-Malo
30 septembre 2022

Une matinée d'interventions sur les instruments de navigation à l'époque de Duguay-Trouin, avec des classes de
cycle 3.
Les journées du patrimoine 2022 à Nantes
les 17 et 18 septembre 2022

- Exposition retraçant les premières années de la Bourse du Travail dans son emplacement
- Instruments de navigation et d’astronomie des origines à nos jours recréés.
- Visites commentées de la tour de l’ancien observatoire de la marine.
La Golden Globe Race 2022
du 20 août au 4 septembre

L'association Méridienne était présente sur le village du 24 août au 4 septembre 2022:
- présentation de re-créations d'instruments de navigation,
- démonstrations d'utilisation du sextant, du quartier de Davis, ... tous les jours à 12h00 heure solaire.
Balade estivale de Nantes Patrimonia
23 août 2022

Une quinzaine de personnes ont suivi cette balade estivale de Nantes Patrimonia, animée par l'association Méridienne.
Festival d'astronomie de la Chapelle aux Lys 2022
20 et 21 août 2022

Exposition de re-créations d'instruments de navigation et d'astronomie..
La 12ème rencontre de 'Coques en bois', à Pornic (44).
11 et 12 juin 2022

Exposition de re-créations d'instruments de navigation et d'astronomie.
École Jacques Brel à Saint-Léger-les-Vignes
7 juin 2022

Intervention dans des classes de CP et de CE1.
Astro 44, à Sautron
7 et 8 mai 2022

Lors de la rencontre annuelle des clubs d’astronomie de Loire-Atlantique, accueillie cette année par Sautron-Astronomie, Méridienne a présenté quelques unes de ses re-créations d'instruments de navigation et d'astronomie.
Les midis du patrimoine, à Nantes
3 février 2022

L'association Méridienne a présenté des re-créations d’instruments de navigation lors de la présentation d'un traité de navigation datant de 1705.
Fête de la science 2021, à Nantes
8, 9 et 10 octobre 2021

Au Museum d'histoire naturelle:
À la découverte des longitudes.
Les journées du patrimoine 2021 à Nantes
18 et 19 septembre 2021

- Présentation du parcours de femmes astronomes et de femmes pirates et corsaires.
- Re-créations d’instruments de navigation et d’astronomie des origines à nos jours.
- Visites commentées de la tour de l’ancien observatoire de la marine.
Festival d'astronomie de la Chapelle aux Lys
les 14 et 15 août 2021

Exposition de re-créations d'instruments de navigation et d'astronomie.
Balade estivale de Nantes Patrimonia
29 juillet 2021

3 adhérents de Méridienne ont animé cette balade estivale de Nantes Patrimonia
La fête du Soleil à Sautron
13 juin 2021

Exposition et présentation de re-créations d’instruments d’astronomie
Fête de la science 2020 à Nantes
samedi 10 octobre 2020

Une balade urbaine au départ du Muséum d'histoire naturelle de Nantes pour évoquer les liens entre l'Homme et la Nature autour de figures nantaises.
Les journées du patrimoine 2020 à Nantes
19 et 20 septembre 2020

- Présentation du parcours de quelques femmes pirates nantaises.
- Re-créations d’instruments de navigation et d’astronomie des origines à nos jours.
Le voyage d'Orient, à Nantes
12 octobre 2019 et 12 février 2020

Dans le cadre de l'exposition Retour d'Orient au muséum, balade historique et scientifique dans Nantes
Fête de la science 2019, à Nantes
5 et 6 octobre 2019

Au Dix:
présentation de re-créations d'instruments d'astronomie et de navigation permettant de se repérer sur le globe terrestre.
Les journées du patrimoine 2019 à Nantes
21 et 22 septembre 2019

- Visites guidées de l'ancien observatoire de la marine.
- Présentation de re-créations d'instruments d'astronomie et de navigation.
Festival d’astronomie de la Chapelle aux Lys
les 10 et 11 août 2019

Exposition de re-créations d'instruments de navigation, centrée sur les voyages de Christophe Colomb.
Les Quarts de Nuit 2019, à St Gilles Croix de Vie (44)
1er août 2019

- Exposition de re-créations d'instruments de navigation.
- Conférence: "Le point en mer, découverte des instruments du 15e au 18e siècle" par Jacques Lehébel.
Maison de l'Université de Rouen (76)
juin et juillet 2019

Participation à l'exposition "Naviguer aux étoiles" par le prêt d'une de nos re-créations.
La réussite d'un concert
31 mai 2019

La caisse à outils de Méridienne a permis à un chanteur de rue de réparer sa guitare...
Francesco a dédicacé une chanson à Méridienne.
La semaine du golfe 2019
du 29 mai au 1er juin 2019

Quatre jours de présentation et de démonstrations de nos re-créations d'instruments d'astronomie et de navigation.
Remise des prix de la Golden Globe Race 2018 aux Sables d'Olonne
22 avril 2019

Deux prix fabriqués par Méridienne, un astrolabe et un quadrant nautique.










