Association Méridienne Atelier
Atelier Le torquet
Le torquet Calculs nécessaires à la construction du torquet
Calculs nécessaires à la construction du torquet
Calculs nécessaires à la construction du torquet
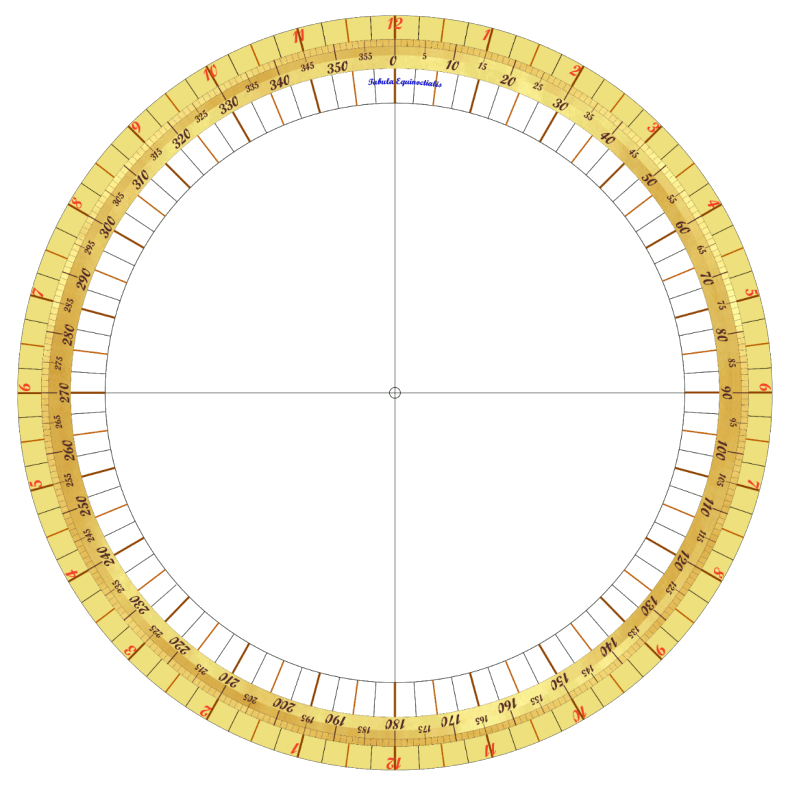
DISQUE ÉQUATEUR Tabula Equinoctialis.
- Sur un disque de 28 cm de diamètre, dans une couronne périphérique (Rexterne = 14 cm,
Rinterne = 13 cm), tracer les graduations des heures et des quarts d'heure en deux fois 12 h.
1 h ↔ 15° ; 15 min ↔ 3,75° - Sur une deuxième couronne (Rexterne = 13 cm, Rinterne = 12 cm) tracer les graduations en degrés de 0° à 360°.
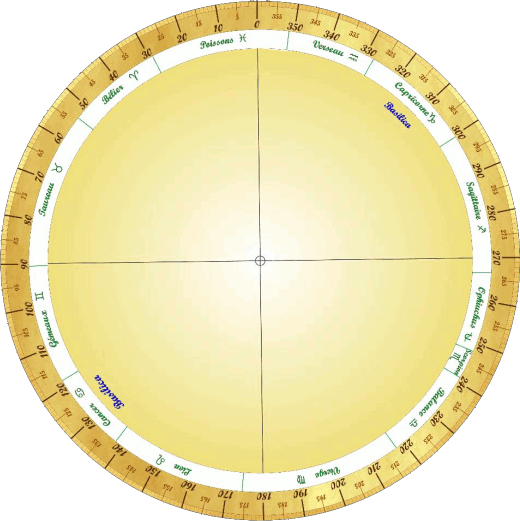
DISQUE BASE Basilica.
- La graduation de cette base découle de la projection de l'écliptique sur le plan de l'Équateur.
Il faut donc convertir les coordonnées écliptiques en coordonnées équatoriales.
tan α = tan λ cos εavec : α = ascension droite en ° λ = longitude écliptique en ° ε = obliquité de l'écliptique = 23°26'
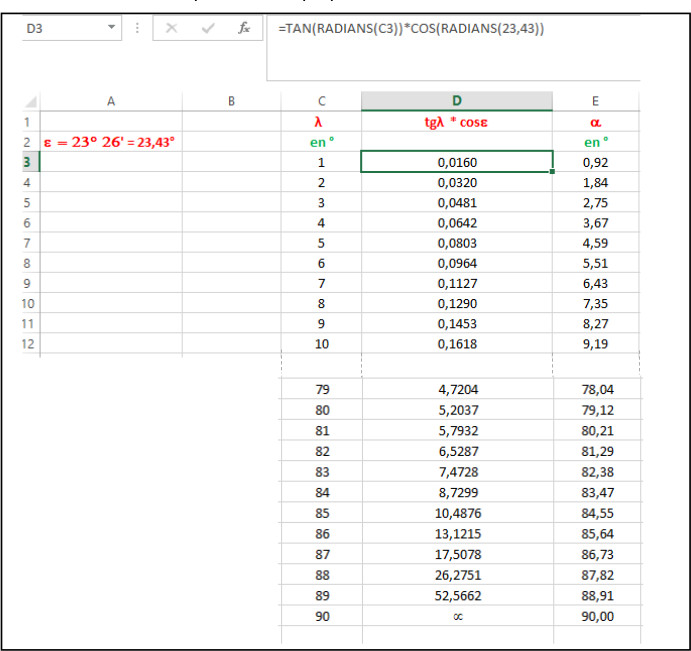 Sur un disque de 22 cm de diamètre, dans une couronne périphérique (Rexterne = 11 cm, Rinterne = 10 cm),
tracer les graduations en degrés de 0° à 360°.
Sur un disque de 22 cm de diamètre, dans une couronne périphérique (Rexterne = 11 cm, Rinterne = 10 cm),
tracer les graduations en degrés de 0° à 360°.
-
Sur une deuxième couronne (Rexterne = 10 cm, Rinterne = 8 cm) tracer le calendrier des constellations
zodiacales.
Le Soleil entre dans la constellation de la /du /des le longitude écliptique* en degrés Capricorne 20 janvier 299,71 Verseau 16 février 327,89 Poissons 12 mars 351,57 Bélier 19 avril 29,09 Taureau 14 mai 53,47 Gémeaux 22 juin 90,43 Cancer 21 juillet 118,26 Lion 11 août 138,18 Vierge 17 septembre 174,16 Balance 31 octobre 217,80 Scorpion 23 novembre 241,14 Ophiuchus 30 novembre 248,04 Sagittaire 18 décembre 266,61
*calendrier astronomique 2019 par Guy Ottewell (www.universalworkshop.com)
DISQUE ÉCLIPTIQUE Rotula Ecliptica.
Ce disque de 22 cm de diamètre contient trois couronnes : une pour les graduations en degrés, une pour le calendrier des constellations zodiacales et une troisième excentrée pour le calendrier.
- Sur une couronne périphérique (Rexterne = 11 cm, Rinterne = 10,2 cm), tracer les graduations en degrés de 0° à 360°.
- Sur une deuxième couronne (Rexterne = 10,2 cm, Rinterne = 9,4 cm) tracer le calendrier des constellations zodiacales. (voir la deuxième couronne du disque de base)
-
Couronne excentrée
- Calculs pour le positionnement du calendrier
Pour mettre en évidence le fait que le Soleil ne paraît pas se déplacer sur l'écliptique d'un mouvement uniforme, dans le courant de l'année, subissant de ce fait une inégalité en longitude, vers 150 ans avant J.-C., le grand astronome grec Hipparque avait imaginé un excentrique (cercle excentrique) dont les éléments lui avaient été fournis par l'inégalité des saisons.
L'Astrolabe de Raymond d'Hollander, pages 126 et 127 (Cf. bibliographie).
On utilise un cycle de quatre années : 2017; 2018; 2019; 2020 (année bissextile).
année 2017 2018 2019 2020 durée moyenne durée en j en j en ° printemps 92 j
+17,557h92 j
+17,557h92 j
+17,557h92 j
+17,557h92,742 91,412 α 92,732 92,744 92,747 92,746 été 93 j
+15,627h93 j
+15,779h93 j
+15,832h93 j
+15,783h93,657 92,314 β 93,651 93,657 93,660 93,658 automne 89 j
+20,436h89 j
+20,478h89 j
+20,588h89 j
+20,528h89,853 88,565 89,852 89,845 89,858 89,855 hiver 88 j
+23,792h88 j
+23,595h88 j
+23,503h88 j
+23,585h88,984 87,659 89,991 89,983 89,979 89,982 total 365,236 360
α + β = 91,412 + 92,314 =183,726°
date 2017 2018 2019 2020 moyenne printemps
le:20 mars
+10h 28min 38s20 mars
+16h 15min 27s20 mars
+21h 58min 25s20 mars
+ 3h 49min 36s20,44 mars 20,68 mars 20,92 mars 20,16 mars 20,55 mars été
le:21 juin
+ 4h 24min 09s21 juin
+10h 07min 18s21 juin
+15h 54min 14s20 juin
+21h 43min 40s21,18 juin 21,42 juin 21,66 juin 20,91 juin 20,29 juin automne
le:22 septembre
+20h 01min 48s23 septembre
+ 1h 54min 05s23 septembre
+ 7h 50min 10s22 septembre
+13h 30min 38s22,83 sept 23,08 sept 23,32 sept 22,56 sept 22,95 sept hiver
le:21 décembre
+16h 27min 57s21 décembre
+22h 22min 44s22 décembre
+ 4h 19min 25s21 décembre
+10h 02min 19s21,69 déc 21,93 déc 22,18 déc 21,42 déc 21,81 déc
E est le centre de l'excentrique, cercle de rayon R supposé être parcouru par le Soleil d'un mouvement uniforme, mais qui ne sera plus perçu comme tel par l'observateur terrestre placé en O, centre de l'écliptique.
L'Astrolabe de Raymond d'Hollander, page 127 (Cf. bibliographie).durée (printemps + été) > 180° et durée (printemps + été) > durée (automne + hiver)
\(\Rarr\) E à droite de la ligne équinoxialedurée été > durée printemps \(\Rarr\) E au-dessus de la ligne solsticiale
λ = longitude écliptique de l'apogée A de la trajectoire apparente du Soleil
À partir du schéma, après divers calculs géométriques* on trouve :
λ = 103,3° et OE = 3 mm
* voir fiche CALCULS COMPLÉMENTAIRES ci-dessous.
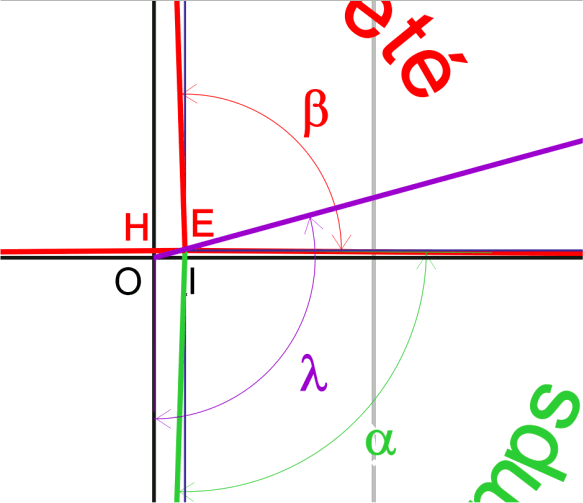
Zoom de la construction pour le positionnement de E
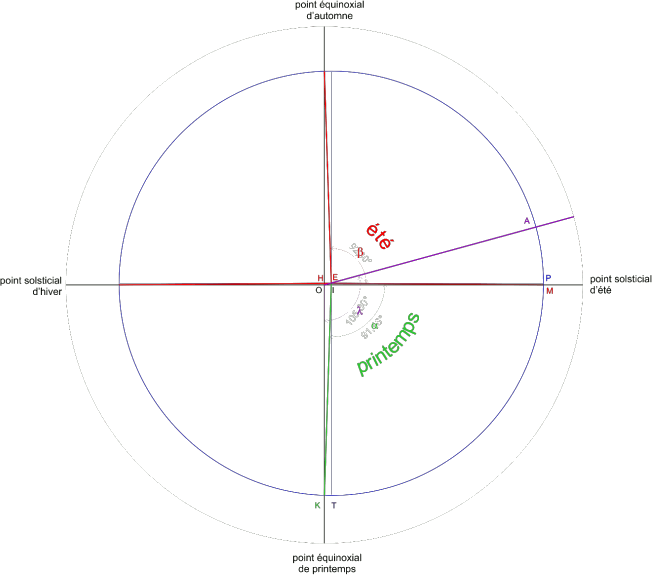
- Tracé du calendrier
Positionner le point E avec précision et tracer le cercle de rayon R = 9 cm.
Sur une couronne (Rexterne = 9 cm, Rinterne = 8 cm) tracer le calendrier en positionnant les points équinoxiaux et les points solsticiaux par rapport à la couronne extérieure graduée en degrés en tenant compte des calculs précédents.
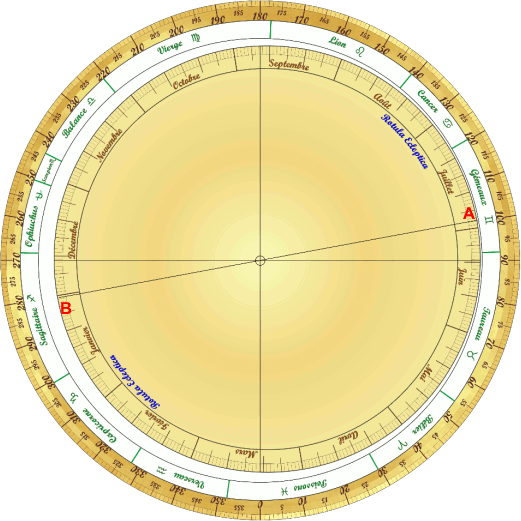
Les points A et B, intersection de la droite (OE) avec le cercle des dates doivent indiquer les dates correspondant au périhélie et à l'aphélie du barycentre du système Terre + Lune.
Pour la Terre seule: Année Périhélie Aphélie Date Heure Date Heure 2017 4 janvier 14:00 3 juillet 20:00 2018 3 janvier 06:00 6 juillet 17:00 2019 3 janvier 05:00 4 juillet 22:00 2020 5 janvier 08:00 4 juillet 12:00
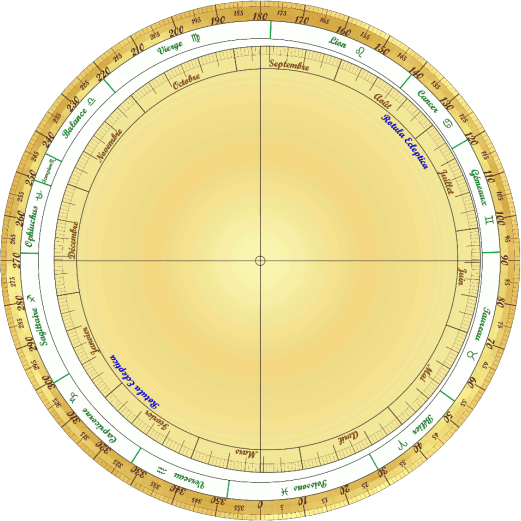
- Calculs pour le positionnement du calendrier
CALCULS COMPLÉMENTAIRES
D'après Raymond d'Hollander, L'Astrolabe pages 127 et 128 (Cf. bibliographie).
Calculs de λ et OE
\( \widehat{\text{KT}} = \dfrac{\alpha + \beta - 180}{2} = 1,863 \degree \)
\( \text{HE} = \text{R}\sin\widehat{\text{KT}} = \text{R} \times 0,0325 \)
\( 2\,\widehat{\text{PM}} = \dfrac{\beta - \alpha}{2} = 0,451\degree \)
\( \text{EI} = \text{R} \sin \widehat{\text{PM}} = \text{R}\times 0,0079 \)
\( \text{OE}^2 = \text{HE}^2 + \text{EI}^2 = \text{R}^2 \times 0,00112 \ \Rightarrow \ \text{OE} = 0,0334\, \text{R} \)
e valeur de l'excentrement : \( \text{e} = \dfrac{\text{OE}}{\text{R}} = \dfrac{0,033\,\text{R}}{\text{R}} = 0,033 = \dfrac{1}{29,899} \)
\( \sin\lambda = \dfrac{\text{HE}}{\text{OE}} = \dfrac{\text{R}\times 0,0325}{\text{R}\times 0,0334} = 0,9731 \ \Rightarrow \ \lambda = 76,668\degree
\quad \text{ou} \quad \lambda = 103,332\degree \)
\( \dfrac{\text{OE}}{\text{R}} = \dfrac{1}{29,899} \ \Rightarrow \ \text{OE} = \dfrac{90}{29,899} = 3,01\,\text{mm} \)
λ = 103,3° et OE = 3 mm
DISQUE CRÊTE Crista.
- Sur un disque de 22 cm de diamètre, dans une couronne périphérique (Rexterne = 11 cm, Rinterne = 9,5 cm), tracer les graduations en degrés quatre
fois 90° (de 0° à 90°; 90° à 0°; 0° à 90° et 90° à 0°).

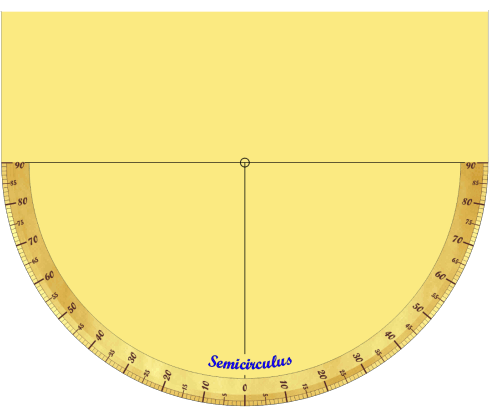
DEMI-DISQUE Semicirculus.
- Sur un demi-disque de 6,2 cm de diamètre, dans une demi-couronne périphérique
(Rexterne = 11 cm, Rinterne = 9,5 cm), tracer les graduations en degrés deux fois 90°
(de 90° à 0°et de 0° à 90°).